1) U svim inercijalnim sistemima svi fizički zakoni formulišu se na istovjetan način;
2) Brzina svjetlosti u vakuumu u svim inercijalnim sistemima jednaka je u svim pravcima i smjerovima i ne zavisi od kretanja sistema ili izvora (svjetlosti).
Postulat – Aksiom, polazna (osnovna) tvrdnja. Tvrdnja koja se ne dokazuje i ne izvodi (ne može se izvesti) iz bilo koje druge tvrdnje, tvrdnja koja je potpuno neovisna o drugim (drugačijim) tvrdnjama. Polazna istina koja proizilazi iz opšteg iskustva i spoznaja stečenih iskustvom i intuicijom. Opšte prihvaćena i ne sumnjiva istina koja je očita (ne sporna), koja se podrazumijeva i kao takva ne dokazuje se (ne treba je dokazivati).
Teoreme (pa i cijela teorija) izvedene iz polaznih aksioma mogu biti formalno pravilne (relativno istinite), ali to nikako ne znači da moraju biti i da jesu objektivno istinite.
U tumačenju i primjeni postulata specijalne teorije relativnosti Alberta Ajnštajna uočio sam začuđujuće mnogo površnosti, nedoslijednosti i protivurječnosti i među matematičarima i među fizičarima! Albert Einstein ne navodi “referentni sistem” u vakuumu u odnosu na koji definiše (iskazuje) brzinu svjetlosti, niti navodi način kako tu izjavu (tvrdnju) možemo potvrditi (provjeriti), kako je postala opšte-prihvaćena i nesumnjiva istina. Po definiciji pojma - postulat (aksiom) Albert Einstein ni po kom kriteriju nije mogao postaviti postulat 2. Taj postulat je i nenaučan, proizvoljan i dat odokativno i sporan je, i nije zasnovan na iskustvu! Prema samoj formulaciji postulata 2 ispada da je svaki sistem nosač brzine c (kao što je svaki vagon voza nosač moje brzine kretanja u njemu).
Postulat 2. treba doslovno shvatiti tako kao što piše u prvom dijelu formulacije - brzina svjetlosti u vakuumu - i nigdje više!
On se može primijeniti na bilo koji objekat ili pojavu koja se kreće u vakuumu nekom svojom brzinom 0 < c < ∞, ili 0 < v < ∞, (0 < v < c < ∞). Na tu brzinu prostiranja u vakuumu nema nikakvog uticaja brzina kretanja u vakuumu “emitera” ili “prijemnika” – detektora (svjetlosti). Ona je takva kakva jeste, inercijalna, kao i brzine svih drugih objekta u vakuumu (dok ne stupe u interakciju sa drugim tijelima, odnosno dok na njih ne počne djelovati neka "nova sila")!
Takva je i brzina prostiranja zvuka u homogenoj materijalnoj sredini. I za zvuk i za svjetlost treba voditi računa da li je sredina prostiranja “nosač” ili nije “nosač” brzine – c.
Sve upućuje na činjenicu da je svjetlost, kao elektromagnetna pojava, nosač “sam sebi”, (magnetna komponenta – nosač električnoj, a električna komponenta – nosač magnetnoj komponenti “elektromagnetnog oscilatora”, i na tom principu su i izvedene Maksvelove formule).
Na emitovanje brzine prostiranja svjetlosti u vakuumu (baš kao i na brzinu prostiranja zvuka u homogenoj materijalnoj sredini) nije moguće primijeniti mehanički “balistički princip”.
Za svjetlost je bitan i drugi detalj: promjenom relativne brzine kretanja (emitera ili detektora) promijenit ćemo opažanje svjetlosti (opažanjem promjene broja pruga u jedinici vremena, opažanjem promjene talasne dužine i frekvencije, ali će nam uvijek umnožak iz frekvencije i talasne dužine dati „brzinu svjetlosti u vakuumu“-c:

To je “fizički osnov” za istinitost i primjenu postulata 2. kada se govori o svjetlosti i njenoj brzini u vakuumu. Drugi fizički osnov za mogućnost primjene postulata 2 u računanjima i algebarskim iskazima odnosi se i na “neku konstantu c ” – koja je aritmetička sredina za relativne brzine (c+v) i (c-v), u kojima nije nužno da brzina c bude brzina svjetlosti u vakuumu.
Osnova za matematičku primjenu tog postulata je odnos između aritmetičke, geometrijske i harmonijske sredine za brzine, vremenske intervale i odgovarajuće dužine. U samim formulama iz oblasti Ajnštajnove STR fizičari nisu uočili “uskrsnuće” baš te „aritmetičke sredine – c“ – za brzine:
(c+v) i (c-v), te aritmetičke sredine t za odgovarajuće dužine i vremenske intervale:
Ta osobina brzine c omogućava nam i postulat 2. i primjenu c = c , ali i primjenu ne samo onda kada je c brzina svjetlosti u vakuumu, već u svim mogućim primjerima brzina: 0 < v < c < ∞ , bilo kojih intenziteta, i konkretno osmišljenih i posmatranih inercijalnih kretanja fizičkih objekata. Tako, na primjer, u ovoj algebarskoj fizičkoj i geometrijskoj istini:
a) (ct + vt) : c = 2t1 , ili , b) (ct – vt) : c = 2t2 , lijevo (ct + vt) je stvarnost, a desno (2ct1 ) je mogućnost (i obratno, u zavisnosti šta i kako konkretno posmatramo i mjerimo, a šta izračunavamo), brzine c i v mogu imati bilo kolike skalarne vrijednosti, brzina c ne mora biti brzina svjetlosti, ali je uvijek veća po intenzitetu od brzine v.
Umjesto stvarne, objektivno istinite, relativne brzine (c + v), ili relativne brzine
(c – v) koristimo mogućnost, moguću brzinu c, kao aritmetičku sredinu na određenoj dužini. Računajući tako, za male vrijednosti brzine v spram brzine c, rezultati računanja će malo i neuočljivo odstupati od izmjerenih (eksperimentalnih) vrijednosti. Međutim, za brzine v većih intenziteta takvo računanje će znatno odstupati od izmjerenih (eksperimentalnih, stvarnih) vrijednosti, te je nužna korekcija ili dužine, ili vremena, ili i jednog i drugog. Najčešća korekcija podrazumijeva: Korekciju i izmjerenih (eksperimentalnih) vrijednosti i algebarskih (geometrijskih) vrijednosti.
Slično (korištenje geometrijske sredine) imamo i u jednoj od važnijih Ajnštajnovih formula (fizička, algebarska i geometrijska istina, koju Ajnštajn pogrešno tumači i primjenjuje, gdje je l0 izmjerena dužina u kretanju brzinom v okomito postavljena na pravac kretanja):
 . Primjenjujući postulat 2. i dijeleći obje strane sa c dobijamo jednu od osnovnih Ajnštajnovih formula:
. Primjenjujući postulat 2. i dijeleći obje strane sa c dobijamo jednu od osnovnih Ajnštajnovih formula:
Formula je tačna i istinita za sve moguće brzine (0 < v < c < ∞) i zbivanja koja posmatramo. Pogrešno je Ajnštajnovo tumačenje fizičke stvarnosti koja se tom formulom opisuje prilikom opisa inercijalnih relativnih kretanja. U navedenom ne postoji i kretanje l0 = ct0 , to je samo mogućnost, koja se može obistiniti i eksperimentalno provjeriti i potvrditi, ali u nekom drugom i drugačijem zbivanju. To je jedan od izrazitih primjera gdje Ajnštajn poluistinu (moguću istinu) protura kao (stvarnu) istinu jednostavnim govornim iskazom: “Njemu će – “unutrašnjem posmatraču će” - proteći vrijeme t0 ”, “kako je c brzina i za unutrašnjeg “posmatrača” onda je…”, “za njega je…”, “on će vidjeti”, “njemu će se dogoditi”, “on će zaključiti”. Sve neki “mutavi posmatrači”, kojima A. Ajnštajn određuje i šta će misliti, šta će vidjeti, šta će biti njihova stvarnost, šta će mjeriti i šta će i kako misliti i zaključivati. Tako ispadne da to u njihovo ime ne razmišlja i zaključuje A. Ajnštajn , već da je to njihova stvarna fizička istina!
U stvarnosti mjerimo samo jedan vremenski interval, vrijeme t1, t2 t, t' ili t0 , druge izračunavamo, kao mogućnost, koja se može ostvariti, obistiniti i eksperimentalno provjeriti i potvrditi. Nikad se konkretno i eksperimentalno u istom fizičkom sadržaju ne mjeri i ne provjeravaju oba vremenska intervala. Za iskazivanje dužina, A. Einstein koristi geometrijsku sredinu brzina i vremenskih intervala. Da bi rezultat takvog prikaza (Ajnštajnovo 2ct') bio što istinitiji nužno je malo povećati/smanjiti vrijeme (u zavisnosti koje vrijeme i koju dužinu mjeri t ili t0 ) i povećati/smanjiti dužinu (u zavisnosti da li mjeri 2ct0 ili ct).
Albert Ajnštajn nije uočio vezu između Aritmetičke sredine (A), Geometrijske sredine (G) i Harmonijske sredine (H) u fizičkim i geometrijskim sadržajima koje opisuje u svojoj STR.
Tu algebarsku, geometrijsku, fizičku i logičku istinu ne uočavaju ni savremeni fizičari i matematičari kada pričaju priču o Ajnštajnovom “crtkanom” vremenu
 ,
, 
ili kada pričaju o Lorencovim koordinatama:
 ,
, 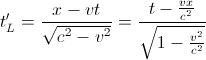
 ,
, 
----------------------------------------------------------
Jedan od popularnih interpretacija Euklidovog petog postulata glasi
V Euklidov postulat
Kroz tačku van prave se može povući tačno jedna prava paralelna sa tom pravom.
Posledica ovog postulata je i da je zbir tri ugla u trouglu jednak zbiru dva prava ugla, da važi Pitagorina teorema i još mnogo trigonometrijskih identiteta. Sve ovo je ukazivalo da je ovaj postulat težak za dokazivanje, ali je stvaran i očigledan. Bilo je rasprostranjeno mišljenje da Euklidova geometrija adekvatno opisuje svet i univerzum.
Geometrija Lobačevskog prihvata sve ostale Euklidove postulate, sem petog, odnosno umesto petog Euklidovog daje svoj postulat koji glasi
V Postulat Lobačevskog
Kroz tačku van prave postoje bar dve prave koje su paralelne sa tom pravom.
Koliko god izgledalo čudno, Lobačevski je dokazao da ovako dobijena geometrija jeste moguća, pa je izveo niz teorema koji važe u novoj geometriji i koristeći matematički aparat prvi put pokazao da je moguće isključivo matematičkom logikom dokazati postojanje potpuno drugačijeg (nama stranog) sveta, iako nismo u stanju da ga svojim čulima spoznamo, pa nam je čak i imaginaciji dalek. Za ovu Geometriju Lobačevskog, koju je sam Lobačevski, za razliku od “obične” ili Euklidove geometrije, nazvao “imaginarna geometrija” kasnije su, međutim, stvoreni i modeli očiglednog predstavljanja, kao što su Klajnov model, Poenkareov disk model iliPoenkareov poluravanski model koji su nazvani prema imenima njihovih autora, matematičara Feliksa Klajna i Anri Poenkarea. Takođe, mada pripada jednoj drugoj vrsti neeuklidske geometrije, očiglednom predstavljanju neeuklidske geometrije doprineo je iBernhard Rimanov sferni model u kojem je neeuklidska ravan predstavljena sferom, a neeuklidske prave su velike kružnice ove sfere (na primer meridijani iscrtani na globusu) .
Inače, Rimanova geometrija razlikuje se od Geometrije Lobačevskog po tome što se u njenom petom postulatu tvrdi da se kroz tačku izvan date prave ne može povući ni jedna prava koja ne seče tu pravu, odnosno koja bi sa njom bila paralelna.
----------------------------------------------
Gornji tekst je kopiran sa Wikipedie. Veliki broj fizičara i matematičara primjenjuje navedene matematičke postavke kao da se fizička stvarnost prilagođava zamišljenoj – imaginarnoj – matematičkoj stvarnosti (matematičkoj analizi i zamišljenim geometrijskim postavkama). Zato neka vas ne čudi raskorak između stvarnog i imaginarnog ( „svijeta Minkowskog“).
Fizička (geometrijska) stvarnost se ne ponaša u skladu sa našim geometrijskim postavkama, već naše postavke (geometrijske modele) slobodno biramo i prilagođavamo za lakši (matematički) prikaz fizičke stvarnosti. Da li ćemo za polazište uzeti Euklidov, Rimanov ili postulat Lobačevskog fizička stvarnost o tome ne vodi računa i neće se promijeniti ni u jednom svom sadržajnom i objektivnom detalju, zbog našeg, slučajnog i slobodnog izbora matematičkog modela, ili odabira sistema referencije.
Mnogi fizičari i matematičari nisu svjesni šta u samom startu predstavlja ovaj Bernhard Rimanov sferni model u kojem je neeuklidska ravan predstavljena sferom, a neeuklidske prave su velike kružnice ove sfere (na primer meridijani iscrtani na globusu).
Ovdje je najpogodniji momenat da istaknem i veoma važan terminološki pojam: zakrivljen prostor, ili zakrivljivanje prostora. Većina onih koji koriste takav izraz nisu ni svjesni da ne koriste pojam prostor u njegovom pravom logičkom i spoznajnom smislu, a kada upotrijebe izraz “zakrivljivanje prostora” kao da nisu svjesni o zakrivljivanju u prostoru (fizičkog sadržaja koji opisuju) a ne zakrivljivanja samog prostora. Također, upotreba izraza “dimenzija” ne upotrebljava se u pravom fizičkom značenju, te svugdje gdje to nije ispravno upotrijebljeno pojam dimenzija zamijenite pojmom parametar, podatak, broj.
Ne postoje “višedimenzionalni prostori”! Ne postoji “svijet Minkovskog”, a “Rimanovim”, “Kalbijevim” i inim prostorima treba dati onaj smisao koji im se daje u polaznim postavkama i realnom (a ne imaginarnom) značenju. O “zakrivljenosti prostora” ne možemo kazati ni jedan podatak bez temelja za te podatke – Euklidove geometrije. Euklid je temelj za sve moguće druge i drugačije postavke (a ne “granični slučaj” “neeuklidskih geometrija”). Cjelokupna priča o STR je priča o logici, a ne priča o fizičkoj stvarnosti. Fizičku stvarnost “zaboli ona stvar” koji ćemo geometrijski model koristiti za njeno (nama lakše) opisivanje. Fizička stvarnost se odvija po svojim prirodnim zakonitostima i neovisno od našeg (slobodnog, i slučajnog) izbora geometrijskog modela (ili inercijalnog poredbenog sistema referencije) za njeno opisivanje.
Priča početa polaznim postavkama o “tri prostorne i jednom vremenskom koordinatom” , u koju je uključena i pomenuta “Rimanova sferna ravan”, i geografski meridijani kao pravci na takvoj “Rimanovoj ravni”, u samom startu primjenjuje pogrešne (polazne) postavke.
Umjesto “četvero-vektora” prostor-vrijeme (tri prostorne i jedna vremenska koordinata) sasvim korektno i po istom principu i matematičkom modelu možemo koristiti “četvero-vektor” vrijeme-prostor (tri vremenske i jednu prostornu koordinatu). Čak je i logičnije koristiti “tri vremenske (t, 2t’ i tv) i jednu prostornu koordinatu” (r- poluprečnik sfere).Također umjesto iskaza (za formule u kojima prikazujemo fizička zbivanja): ” c je brzina svjetlosti u vakuumu” , možemo koristiti iskaz: c je najveća moguća brzina u posmatranom fizičkom zbivanju (0 < v < c < ∞), ili c je konačna (trenutna) brzina u posmatranom fizičkom sadržaju!
U samoj STR Ajnštajnov iskaz o dilataciji vremena: možemo zamijeniti “dilatacijom izmjerene dužine” , a kontrakciju dužine možemo zamijeniti “kontrakcijom izmjerenog vremena”, i navedene formule će opet važiti.
Albert Ajnštajn svojim stavom da dužine okomite na pravac kretanja ne mijenjaju svoju dužinu, te interpretacijom x-ose kao pravca u pravouglom koordinatnom sistemu, u svojoj osnovi utemeljuje Euklidovu geometriju i Euklidov stav o paralelnim pravcima. Međutim u primjeni te okomite dužine “zakrivljuje” ih, i/ili “skraćuje” ih ( u zavisnosti od “vremenske” ili “prostorne” koordinate), i u zavisnosti šta mu je u konkretnom primjeru potrebno!
Zato ponovo naglašavam: Nema dilatacije vremena, nema kontrakcije dužina, nema zakrivljivanja prostora, nema zakrivljavanja vremena, nema promjene mase tijela sa promjenom njegove brzine kretanja!

Nema komentara:
Objavi komentar