Sve vezano za pojmove zakona puta podsjetite se sa ovog linaka.
Za razumijevanje (shvatanje, poimanje, iskazivanje) zakona puta: 1) lc = c∙t (bilo čega, bilo kada, bilo gdje, u odnosu na bilo šta, za bilo koga) ne treba nam "viša matematika", "matrice", "kvadrivektori", "diferencijalni račun", "tenzorski račun", "vektorska algebra", "koordinatni sistemi", "inercijalni sistemi referencije", "posmatrači", "odricanje od dosadašnjih shvatanja pojmova prostora i vremena", "geometrija Lobačevskog", "Rimanovi prostori", "Kalabijevi prostori", "posebne jedinice mjere"...., A. Einstein, H. A. Lorentz, J. C. Maxwell,....
Ljudska svijest, formirana intuicijom pravilno shvata pojam dužina puta = lc = ct, u skladu sa Keplerovim, Njutnovim i Galilejevim zakonima kretanja, u skladu sa Euklidovom geometrijom, bez ikakve potrebe za uvođenjem Ajnštajnovih iskaza o "dilataciji vremena" i "kontrakciji dužina". Za "relativističku algebru" proizvod (produkt) mjernog broja brzine c i mjernog broja vremena t ima značenja:
dužina linije (prave ili krive) lc = ct, dužina puta sc = ct, dužina poluprečnika sfere r = ct.
U svim pojmovima (linija, putanja, put, poluprečnik, koordinata) pojam dužina kao fizička, geometrijska i matematička (algebarska) veličina ima isto značenje i smisao.
Ako imamo još neku brzinu v = c/n , (n > 1), n = c/v, c = n∙v, onda će za to isto vrijeme:
t = lc/c proizvod mjernih brojeva brzine v i vremena t dati n puta manju dužinu (puta, linije, poluprečnika):
lv = vt = ct/n = lc/n.
Za razumijevanje (shvatanje, poimanje, iskazivanje) zakona puta: 1) lc = c∙t (bilo čega, bilo kada, bilo gdje, u odnosu na bilo šta, za bilo koga) ne treba nam "viša matematika", "matrice", "kvadrivektori", "diferencijalni račun", "tenzorski račun", "vektorska algebra", "koordinatni sistemi", "inercijalni sistemi referencije", "posmatrači", "odricanje od dosadašnjih shvatanja pojmova prostora i vremena", "geometrija Lobačevskog", "Rimanovi prostori", "Kalabijevi prostori", "posebne jedinice mjere"...., A. Einstein, H. A. Lorentz, J. C. Maxwell,....
Ljudska svijest, formirana intuicijom pravilno shvata pojam dužina puta = lc = ct, u skladu sa Keplerovim, Njutnovim i Galilejevim zakonima kretanja, u skladu sa Euklidovom geometrijom, bez ikakve potrebe za uvođenjem Ajnštajnovih iskaza o "dilataciji vremena" i "kontrakciji dužina". Za "relativističku algebru" proizvod (produkt) mjernog broja brzine c i mjernog broja vremena t ima značenja:
dužina linije (prave ili krive) lc = ct, dužina puta sc = ct, dužina poluprečnika sfere r = ct.
U svim pojmovima (linija, putanja, put, poluprečnik, koordinata) pojam dužina kao fizička, geometrijska i matematička (algebarska) veličina ima isto značenje i smisao.
Ako imamo još neku brzinu v = c/n , (n > 1), n = c/v, c = n∙v, onda će za to isto vrijeme:
t = lc/c proizvod mjernih brojeva brzine v i vremena t dati n puta manju dužinu (puta, linije, poluprečnika):
lv = vt = ct/n = lc/n.
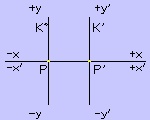
Kada odaberemo početnu tačku P , već smo odredili i “sistem u mirovanju” -
S0 i koordinatni sistem K° čiji je koordinatni početak u toj tački P. U odnosu na tu tačku iskazujemo zakone puta “inercijalnih kretanja”: PP’ = vt i PC = ct.
Opredijelimo se da ovim algebarskim iskazima opisujemo geometrijski opis fizičkih zbivanja:
· Jednolikomonotono pravolinijsko kretanje brzinom v > 0 tokom vremena t >0 u odnosu na tačku P.
· Jednolikomonotono pravolinijsko kretanje brzinom c > 0 tokom vremena t > 0 u odnosu na tačku P.
Dogovorimo se i o intenzitetu (“skalarnim vrijednostima”) brzina:
0 < v < c < ∞ . U tom slučaju, na osnovu iskustva stečenog posmatranjima zaključujemo da su:
1. dužine puta direktno proporcionalne brzinama za isto vrijeme:
PC : PP’ = ct : vt = c : v = n, te da je n = c/v ;
2. Iste, jednake, dužine puta mogu se ostvariti različitim brzinama za različita vremena, te da su vremena obrnuto proporcionalna brzinama na istoj dužini puta. Na primjer:
PP’ : v = t , PP’ : c = tv .
PP’ : v = t , PP’ : c = tv .
c : v = t : tv = n , vt = ctv = PP’ , c = n∙v, t = n∙tv .
Iz navedenih zakona puta: PC = ct i PP’ = vt, koristeći se algebrom sedmog razreda osnovne škole i “Euklidskom geometrijom” , izvest ću vam formule Lorentzovih transformacija (“Lorencove transformacije koordinata”), Ajnštajnove formule u STR, zakone puta za jednakopromjenljiva kretanja (sa ili bez “početne brzine”), te istim formulama ( sa istim oznakama i značenjima) izračunavati mnoge veličine i njihove međusobne relativne odnose i u drugim oblastima fizike (Snelijusov zakon loma, prelamanje svjetlosti, kružna kretanja,..., energije, impuls, ...) i geometrije (trigonometrija i trigonometrijske veličine,...).
Svaka naredna formula (algebarski iskaz) proizilazi iz prethodnih, jasnih i nedvosmislenih “algebarskih zapisa geometrijskog opisa fizičkih zbivanja”. Svaka naredna formula kao da “izvire” iz prethodne, svaka naredna formula je kao rijeka u koju se uljevaju prethodne rječice i pojedinačni izvori. Od kojeg god izvora krenemo stići ćemo do “opštih formula” koje ih objedinjuju, koje u sebi sadrže svu suštinu i smisao prethodnih.
U tome i jeste ljepota “relativističke algebre”: jednostavnost, sklad, logičnost i univerzalnost primjene.
Jednom upotrijebljena oznaka ili formula zadržava svoj smisao i oblik i u narednim algebarskim zapisima (formulama). Zbog toga “relativistička algebra” olakšava učenje, razumijevanje i pamćenje naučenog.
Ukoliko ste ljubopitljivi, ukoliko imate hrabrosti misliti vlastitom ( a ne tuđom) glavom, čitajte dalje!
Sumnja je poželjna! Provjeravate i uvjerite se! Vjerujte sebi i vlastitom shvatanju prostora i vremena!
Nema komentara:
Objavi komentar